5.1 The Gibbs Distribution

Take-home message: The Boltzmann distribution is modified if the particle number can change

Now we consider systems which are in contact with a heat bath at temperature $T$ and also in with a particle reservoir at chemical potential $\mu$. The temperature is a measure of the decrease in entropy of the reservoir from giving up heat to the system (see here); the chemical potential is a measure of the energy decrease (and entropy increase) of the reservoir from giving up particles to the system

We want to find the probability that our system will be in a certain microstate $i$ with an energy $\varepsilon_i$ and particle number $N_i$.

The derivation follows that of the Boltzmann distribution closely. Again the probability of the system being in the given microstate depends on the number of microstates available to the reservoir with energy $E_0-\varepsilon_i$ and particle number $N_0-N_i$. Expressing the number of microstates as the exponential of the entropy, making a Taylor expansion of the entropy about $S_R(E_0,N_0)$, and expressing the derivatives of the entropy in terms of $T$ and $\mu$ thus,

$$\left({\partial S_R\over\partial E}\right)_{\!\scriptstyle V... ...S_R\over\partial N}\right)_{\!\scriptstyle E,V}=-{\mu\over T},$$

gives

$\mbox{\LARGE\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle p_i={e^{ (\mu N_i-\varepsilon_i)/k_{\scriptscriptstyle B}T} \over {\cal Z}}$ }}$

with

$\mbox{\LARGE\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle {\cal Z}=\sum_j e^{ (\mu N_j-\varepsilon_j)/k_{\scriptscriptstyle B}T}$ }}$

The new normalisation constant ${\cal Z}$ is called the grand partition function. Macroscopic functions of state are calculated via ensemble averages as usual; the relevant ensemble in this case is called the grand canonical ensemble.

The following properties are easily proved by analogy with the corresponding ones for the Boltzmann distribution (see here and here):

$$\begin{eqnarray*} \left\langle N \right\rangle \!\!\!&=&\!\!\!k_{\scriptscriptst... ...riptstyle B}T \ln{\cal Z}=\left\langle E-TS-\mu N \right\rangle \end{eqnarray*}$$

The quantity $-k_{\scriptscriptstyle B}T \ln{\cal Z}$ is a new thermodynamic potential called the grand potential: Mandl gives it the unfortunate symbol $\Omega$ but we will use $\Phi_G$ like Bowley and Sánchez. (They use $\Xi$-``Xi''-for ${\cal Z}$.) From the fundamental thermodynamic relation we get

$${\rm d}\Phi_G=- S {\rm d}T-P {\rm d}V-N{\rm d}\mu$$

and hence

$$S=-\left({\partial \Phi_G\over\partial T}\right)_{\!\scripts... ...{\partial \Phi_G\over\partial \mu}\right)_{\!\scriptstyle T,V}$$

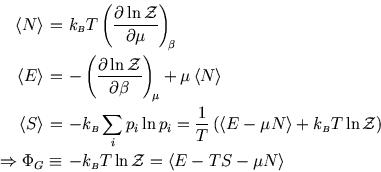
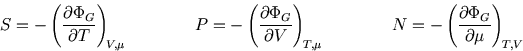
So whereas in an isolated system the entropy is the key (compare here) and in a system at constant temperature it is the Helmholtz free energy (compare here), here the grand potential is the key to the other functions of state.

See here for more details about $\Phi_G$.

References

• Mandl 11.1
• Bowley and Sánchez 69.7-9
• Kittel and Kroemer 5