



Next: 4.7 Translational energy of a molecule
Previous: 4.5 Adiabatic demagnetisation and the third
4.6 Vibrational and rotational energy of a diatomic molecule
So far we have only looked at two-level systems such as the paramagnet. More usually there are many
or even infinitely many levels, and hence terms in the partition function.
In some special cases the partition function can still be expressed in closed form.
Vibrational energy of a diatomic molecule
The energy levels of a quantum simple harmonic oscillator of frequency 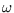 are
are
so
where we have used the expression for the sum of a geometric series,
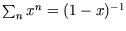 , with
, with
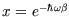 .
.
From this we obtain
The low temperature limit of this (
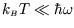 ;
;
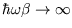 )
is
)
is
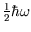 , which is what we expect if only the ground state is populated.
The
high temperature limit (
, which is what we expect if only the ground state is populated.
The
high temperature limit (
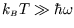 ;
;
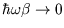 ) is
) is
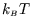 , which should ring bells!
(See here for more on limits.)
, which should ring bells!
(See here for more on limits.)
Typically the high temperature limit is only reached around 1000 K
Rotational energy of a diatomic molecule
The energy levels of a rigid rotor of moment of inertia 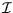 are
are
but there is a complication; as well as the quantum number 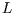 there is
there is 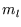 ,
,
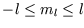 , and the energy
doesn't depend on
, and the energy
doesn't depend on 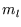 . Thus the
. Thus the 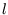 th energy level occurs
th energy level occurs 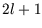 times in the partition function, giving
times in the partition function, giving
The term 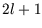 is called a degeneracy factor since ``degenerate'' levels are levels with the same
energy. (I can't explain this bizarre usage, but it is standard.)
For general
is called a degeneracy factor since ``degenerate'' levels are levels with the same
energy. (I can't explain this bizarre usage, but it is standard.)
For general 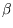 this cannot be further simplified. At low temperatures successive term in
this cannot be further simplified. At low temperatures successive term in 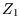 will fall off
quickly; only the lowest levels will
have any significant occupation probability and the average energy will tend to zero.
will fall off
quickly; only the lowest levels will
have any significant occupation probability and the average energy will tend to zero.
At high temperatures, (
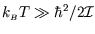 ) there are many accessible levels and the fact that they
are discrete rather than continuous is unimportant; we can replace the sum over
) there are many accessible levels and the fact that they
are discrete rather than continuous is unimportant; we can replace the sum over 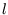 with an integral
with an integral 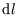 ;
changing variables to
;
changing variables to 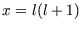 gives
gives
Typically
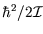 is around
is around 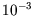 eV, so the high-temperature limit
is reached well below room temperature.
eV, so the high-temperature limit
is reached well below room temperature.
It is not an accident that the high-temperature limit of the energy was
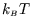 in both cases!
These are examples of equipartition which is the subject of a future section.
in both cases!
These are examples of equipartition which is the subject of a future section.
References
- (Bowley and Sánchez 5.11,5.12)




Next: 4.7 Translational energy of a molecule
Previous: 4.5 Adiabatic demagnetisation and the third
Judith McGovern
2004-03-17
![]() are
are
![]() are
are
![]() ) there are many accessible levels and the fact that they
are discrete rather than continuous is unimportant; we can replace the sum over
) there are many accessible levels and the fact that they
are discrete rather than continuous is unimportant; we can replace the sum over ![]() with an integral
with an integral ![]() ;
changing variables to
;
changing variables to ![]() gives
gives
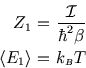
![]() in both cases!
These are examples of equipartition which is the subject of a future section.
in both cases!
These are examples of equipartition which is the subject of a future section.