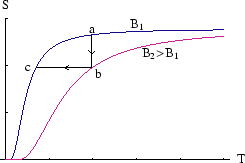
By magnetising and demagnetising a paramagnetic sample while controlling the heat flow, we can lower its temperature.

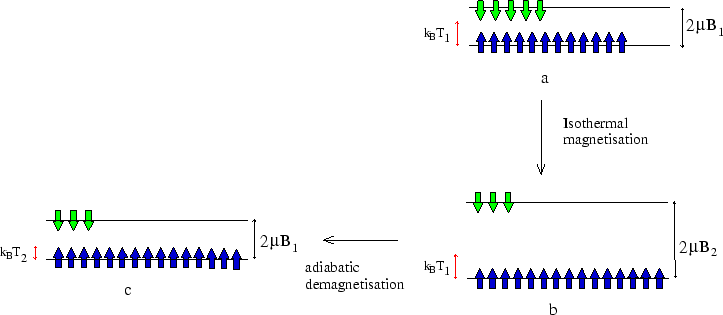
a![]() b: With the sample in contact with a heat bath at
b: With the sample in contact with a heat bath at ![]() , we increase the magnetic field
to
, we increase the magnetic field
to ![]() .
.
b![]() c: With the sample now isolated, we slowly decrease the field to
c: With the sample now isolated, we slowly decrease the field to ![]() again. This is the adiabatic
demagnetisation step; because the process is slow and adiabatic, the entropy is unchanged.
again. This is the adiabatic
demagnetisation step; because the process is slow and adiabatic, the entropy is unchanged.
By following these steps on a ![]() plot, we see that the second, constant entropy, step, reduces the temperature.
The entropy is a function of
plot, we see that the second, constant entropy, step, reduces the temperature.
The entropy is a function of ![]() only, not
only, not ![]() or
or ![]() separately (see here)
so if we reduce
separately (see here)
so if we reduce ![]() at constant
at constant ![]() , we reduce
, we reduce ![]() also.
also.
The following figure shows what is happening to the spins.
If we start with a large sample, we could repeat the process with a small sub-sample, the remaining material acting
as a heat bath during the next magnetisation. By this method temperatures of a fraction of a Kelvin can be reached.
However after a few steps less and less is gained each time, as the curves come together as ![]() .
(Once the electron spins are all ordered, one can start to order the nuclear spins, and reach even lower
temperatures--the magnetic moment of the nucleus is around a two-thousandth of that of the atom), but even that
has its limits.
(Wondering why we can't just take
.
(Once the electron spins are all ordered, one can start to order the nuclear spins, and reach even lower
temperatures--the magnetic moment of the nucleus is around a two-thousandth of that of the atom), but even that
has its limits.
(Wondering why we can't just take ![]() to zero? See here for the real paramagnet.)
to zero? See here for the real paramagnet.)
This is an important and general result. There is always a minimum excitation energy ![]() of the system, and
once
of the system, and
once
![]() there is no further way of lowering the temperature. The unattainability of absolute
zero is the third law of thermodynamics.
there is no further way of lowering the temperature. The unattainability of absolute
zero is the third law of thermodynamics.

References