Derivation of the Boltzmann distribution

We consider a system $S$ in contact with a heat reservoir $R$, the whole forming an isolated system with energy $E_0$.

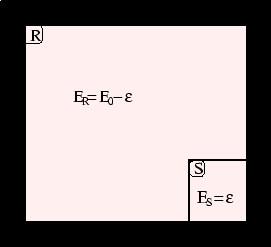
Heat can be exchanged between the system and reservoir, and the likelihood of a particular partition depends on the number of microstates of the whole system $S+R$ corresponding to that partition. (The equilibrium partition will be the one which maximises the number of microstates, but that is not what we are interested in here.) Since the system and reservoir are independent, the total number of microstates factorises: $\Omega=\Omega_S\Omega_R$

Now suppose we specify the microstate of $S$ that we are interested in, say the $i$th (with energy $\varepsilon_i$) and ask what the probability $p_i$ of finding the system in that microstate is. It will be proportional to the number of microstates $\Omega(E_0,\varepsilon_i)$ of the whole system $S+R$. However $\Omega_S=1$ as we've specified the state of $S$, so $\Omega(E_0,\varepsilon_i)=\Omega_R(E_0-\varepsilon_i)$

Using the relation between $\Omega$ and entropy, we can write

$$p_i\propto \Omega_R(E_0-\varepsilon_i)=\exp\{S_R(E_0-\varepsilon_i)/k_{\scriptscriptstyle B}\}$$

If $R$ is to be a good reservoir, it must be much bigger than $S$, so $\varepsilon_i\ll E_0$. Thus we can expand $S_R$ about $S_R(E_0)$ and keep only the lowest terms:

$$S_R(E_0-\varepsilon_i)=S_R(E_0)-\varepsilon_i \left({\partial S_R \over \partial E}\right)_{\!\scriptstyle V,N} +\ldots$$

But the derivative of S with respect to E is just the inverse of the temperature, so we have

$$p_i\propto \exp\{S_R(E_0)/k_{\scriptscriptstyle B}-\varepsil... ...T)\}\propto \exp\{-\varepsilon_i/(k_{\scriptscriptstyle B}T)\}$$

(since $S_R(E_0)$ is a constant, independent of the microstate we are interested in). Calling the constant of proportionality $1/Z$, this is our result:

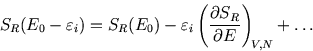
$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle p_i={e^{-\varepsilon_i/k_{\scriptscriptstyle B}T} \over Z}$ }}$

The normalisation constant $Z$ is found by saying that the probability that the system is in some microstate is one: $\sum_j p_j =1$, so

$$Z=\sum_j e^{-\varepsilon_j/k_{\scriptscriptstyle B}T}$$