PC2352 Examples 9&10

21.

Consider the three-level system of question 13, with non-degenerate single-particle energy levels 0, 0.02 and 0.05 eV, in thermal equilibrium with a heat reservoir. In this question, the system contains two particles. For the cases of (a) distinguishable and (b) indistinguishable paticles, calculate the partition function, the average energy of the system at $20^\circ$C and the average energy at $kT»0.05$ eV.

See here for the difference between distinguishable and indistinguishable particles. Note that for the latter there are too few energy levels to use $Z_{\scriptscriptstyle N}=(Z_1)^N/N!$, instead we have to count each two-particle microstate individually.

22.

The density of states for a 2-dimensional gas confined in a square of area $A$ is

$$D(k)={A k\over 2\pi}.$$

a)

By using arguments similar to those given in lectures, derive this relation. (But if you find that hard, don't give up on the rest of the question!)

b)

Use the expression for $D(k)$ to show that at room temperature the partition function for the translational energy of a particle in a macroscopic 2-dimensional box is $Z_1=A\sigma_{{\scriptscriptstyle Q}}$, where $\sigma_{{\scriptscriptstyle Q}}=n_{\scriptscriptstyle Q}^{2/3}=mk_{\scriptscriptstyle B}T/2\pi\hbar^2$. Hence show that the average energy of the particle is $k_{\scriptscriptstyle B}T$, and explain the result.

c)

If there are $N$ indistinguishable particles in the box, and $N/A\ll \sigma_{{\scriptscriptstyle Q}}$, write down the partition function for the system and find its entropy.

d)

Now let the particles have spin ${\textstyle \frac 1 2}$, so that in the absence of an external magnetic field each energy level has a degeneracy of two (spin up and spin down). The effect of this is to double the density of states. How does the entropy change? Explain your result.

This question closely follows the derivation in three dimensions, see here for the density of states and $Z_1$, and here for $S$.

23.

PC235, 2000. Define the Helmholtz free energy $F$ and indicate how the entropy and pressure can be determined if $F$ is known.

A vessel of volume $V$ contains a gas of $N$ highly relativistic spin-zero indistinguishable particles (i.e. their wavenumber $k$ and kinetic energy $\epsilon$ are related by $\epsilon=\hbar ck$). Show that the single particle partition function of the system is given by

$$z={V\over \pi^2}\left({k_{\scriptscriptstyle B}T\over \hbar c}\right)^3.$$

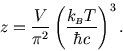
Show that the entropy of the gas in the classical limit is given by

$$S=Nk_{\scriptscriptstyle B}\left(\ln\left({z\over N}\right)+4\right).$$

Calculate the pressure and internal energy and comment on the results.

[You may assume that the density of states is given by $D(k)=Vk^2/(2\pi^2)$,
and that $\int_0^\infty x^n{\rm e}^{-x}{\rm d}x=n!$
You may use Stirling's approximation, $\ln N!=N\ln N-N$.]

Once again this closely follows the derivation for a non-relativistic particle; the density of states is the same, but the actual integral that has to be done to get $Z_1$ is an exponential rather than a Gaussian.

24.

A given system, of fixed volume, is in contact with a heat and particle reservoir.

(a)

Show that

$${\left\langle N \right\rangle } = \sum_{r} N_{r} p_{r} = kT \left. \frac{\partial } {\partial \mu} \left( \ln {\cal Z} \right) \right\vert _{T,V}$$

$${\rm and } {\left\langle E \right\rangle } = \sum_{r} E_{r} p_{r} = - \left. \frac{\partial }{\partial \beta... ... \ln {\cal Z} \right) \right\vert _{V,\mu} + \mu{\left\langle N \right\rangle }$$

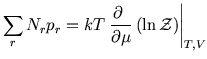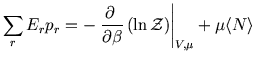where the symbols have their usual meanings.

(b)

Using the general definition of entropy, $S = - k\sum_r p_r \ln p_r$, show that for a macroscopic system,

$$\Phi_{\scriptscriptstyle G}= E - TS - \mu N {\rm where } \Phi_{\scriptscriptstyle G}= -kT\ln {\cal Z}.$$

These closely follow the derivations in the Boltmann case, here for $\left\langle E \right\rangle$ and here for $S$.

(c)

Show that $\Phi_{\scriptscriptstyle G}= - PV$.

See here.