PHYS20672 Summary 3

Cauchy's theorem

  1. Stokes's theorem states that for a closed path $C$ in the $xy$ plane enclosing a surface $S$, $$\oint_C (A_x \d x+A_y\d y)=\int\!\!\int_S\left(\pdby{A_y}x-\pdby{A_x}y\right)\d x\,\d y$$
  2. Hence Cauchy's theorem: if $f(z)$ is analytic, so that $\dslby fz=\pdslby fx = -\ii\pdslby fy$, $$\oint_C f(z) \d z=\oint_C(f\d x+\ii f\d y)=\int\!\!\int_S\left(\ii\pdby fx - \pdby fy\right)\d x\,\d y=0$$
  3. From this it follows that the integral of a function between two points is path independent, if and only if the function is analytic in the closed region bounded by the two curves.
  4. If the integral $F(z)=\int_a^z f(\xi)\d\xi$ is independent of the path taken from $a$ to $z$, then $\d F/\d z=f(z)$.
  5. The indefinite integral $\int^z f(\xi)\d\xi$ doesn't depend on a fixed starting point, and hence is only defined up to an additive constant.
  6. If a function is analytic in some region, a closed contour can be deformed at will within that region without changing the value of the integral along it.
  7. If a function within a contour is analytic except at a finite number of isolated points, the integral round that contour is the same as the sum of the integrals round a set of contours each of which circles just one singularity. In the diagram below, $\oint_C\to\oint_{C_1}+\oint_{C_2}+\oint_{C_3}$.
  8. $\oint 1/(z-a)\d z=2\pi i$; $\oint (z-a)^n\,\d z=0$ for integer $n\ne-1$.

image of mappings

Spiegel 4.9,4.11,4.13-15

Riley 18.11; Boas 14.3; Arfken 6.3

Cauchy's integral formulae

  1. Cauchy's integral formulae are $$ f(a)=\frac{1}{2\pi i}\oint \frac{f(z)}{z-a}\d z\qquad\text{and}\qquad f^{(n)}(a)=\frac{n!}{2\pi i }\oint \frac{f(z)}{(z-a)^{n+1}}\d z$$ where $f^{(n)}(a)$ is the $n$-th derivative of $f(z)$ evaluated at $z=a$.
  2. All derivatives of $f$ are also analytic functions in the region where $f$ is analytic
  3. If $f(z)$ is analytic and bounded on the entire complex plane, it must be constant (Liouville's theorem).
  4. The fundamental theorem of algebra states that any polynomial of degree $n$ must have $n$ roots (not necessarily all distinct)
  5. The (generalized) argument theorem states that if, within a closed curve, a function has $N$ zeros and $P$ poles (with a double root or pole counting as 2, etc.) then $$\oint\;\frac{f'(z)}{f(z)}\d z = 2\pi i(N-P).$$

Spiegel 5.1-2

Riley 18.12; Boas 14.3; Arfken 6.4

Taylor and Laurent Series

  1. If a function $f(z)$ is analytic within a circle radius $R$ centred on $a$, then according to Taylor's theorem we can write $f(z)$ as a power series $$f(z)=f(a)+f'(a)(z-a)+f''(a)(z-a)^2/2!+\ldots+f^{(n)}(a)(z-a)^n/n!+\ldots.$$
  2. The radius of convergence, $R$, will be set by the position of the singularity (e.g. a pole or branch point) that is closest to $a$.
  3. If in a Taylor series the coefficients of the first $n$ terms vanish, $f(z)$ has a zero of order $n$ at $z=a$.
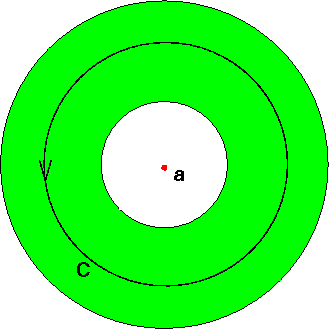  4. image of contour for Laurent seriesIf a function $f(z)$ is analytic within an annulus of inner radius $R_1$ and outer radius $R_2$ centred on $a$, then according to Laurent's theorem we can write $f(z)$ as follows: $$f(z) = \sum_{n=0}^\infty a_n(z-a)^n + \sum_{n=1}^\infty\frac{b_n}{(z-a)^n},$$ where, taking the path of integration to lie in the annulus (and encircling $a$), $$a_n=\frac{1}{2\pi i}\oint \frac{f(z)}{(z-a)^{n+1}}\d z\qquad\text{and}\qquad b_n=\frac{1}{2\pi i}\oint\; f(z)(z-a)^{n-1}\d z.$$ The first series is called the regular (or analytic) part of $f(z)$ and the second the principal part.

  5. If $b_m=0$ for all $m$, the series is just the Taylor series; however, this will be true only if $f(z)$ is in fact analytic inside the inner radius of the annulus.
  6. If $z=a$ is an isolated singularity (so not a branch point) of $f(z)$, we can form a Laurent series about $z=a$ which is valid for $0 < |z-a| < R$ where $R$ is the distance to the next singularity. If the principal part terminates, so that $b_m=0$ for all $m > n$, we say $f(z)$ has a pole of order $n$ at $z=a$. If $n=1$ we call it a simple pole. If there is no such value $n$, $z=a$ is an essential singularity. $e^{1/z}$ is an example of a function with an essential singularity at $z=0$.
  7. An entire function is analytic everywhere in the finite complex plane; its Taylor series about any point $z=a$ has infinite radius of convergence. $e^z$ is an example of an entire function.
  8. A meromorphic function is one that is analytic (in a given region of the complex plane), except for a set of isolated points that are poles of the function. $1/\sin z$ is an example of a meromorphic function: it has simple poles at $z=n\pi$ on the real axis.
  9. Define $w=1/z$ and $g(w)=f(1/w)$. Then the nature of any singularity of $g$ at $w=0$ is the nature of any singularity of $f$ at infinity. For example, $f(z)=z$ has a simple pole at infinity, because $f(1/w)=1/w$ has a simple pole at $w=0$. Similarly, $e^z$ has an essential singularity at infinity.

Spiegel 6.1-5, (6.6), 6.7-12

Riley (18.4, 18.6), 18.13; Boas 14.4, 14.8; Arfken 6.5, 7.1