PHYS20672 Summary 2

Conformal mappings

1. If $u(x,y)+\ii v(x,y)$ is an analytic function of $z=x+\ii y$, contours of constant $u$ and $v$ intersect each other at right angles in the $z$-plane at every point where $f'(z)\ne0$.
2. If $f$ is analytic, the mapping $w=f(z)$ preserves angles and, for sufficiently small regions, shapes, wherever $f'(z)\ne0$. The mapping is called conformal.
3. Suppose we wish to find $u(x,y)$, the solution to Laplace's equation $\del^2u=0$ subject to certain boundary conditions, and that the mapping $Z=X+\ii Y=f(z)$ maps the boundaries to a new, simpler geometry in which Laplace's equation can be solved to give the potential function $\Phi(X,Y)$. Then $u(x,y)=\Phi(X(x,y),Y(x,y))$ will be the solution to the original problem.
4. If $\Psi(X,Y)$ is conjugate to $\Phi(X,Y)$ (i.e., if $\Phi+\ii\Psi$ is an analytic function of $Z=X+\ii Y$), lines of constant $v(x,y)=\Psi(X(x,y),Y(x,y))$ represent field lines, lines of heat flow or streamlines according to the physical interpretation of the function $u(x,y)$. The analytic function $u+\ii v$ is called the "complex potential".

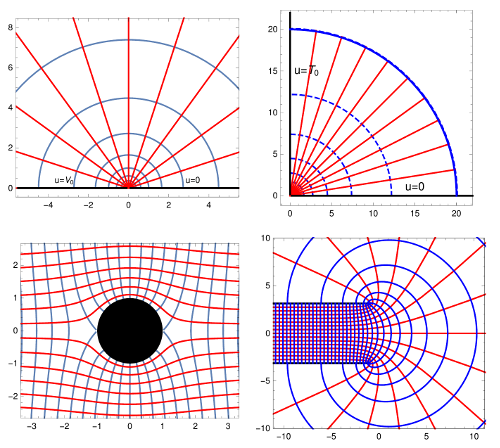
In the diagrams above, the coloured lines are equipotentials and flow/field lines for a variety of problems.

Riley 18.7-9; Boas 14.9, 14.10; (Arfken 6.7)

Integration in the complex plane

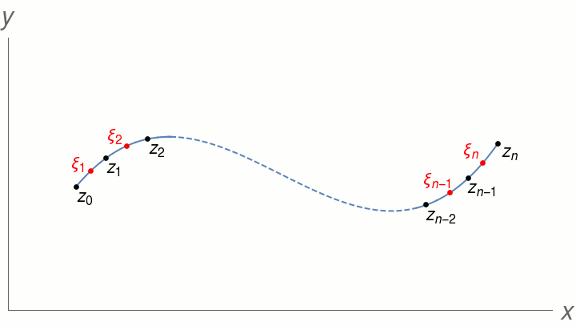
1. The path (or contour) integral of a complex function is defined as $$\int_C f(z)\,\d z=\lim_{n\to\infty}\sum_{k=1}^{n} f(\xi_k)(z_k-z_{k-1}),$$ where $z_0$ and $z_n$ are the end-points of the contour, the other $z_k$ are points distributed in order along the contour, and the points $\xi_k$ are chosen to lie between $z_{k-1}$ and $z_k$ on the contour. Provided $f(z)$ is continuous and the limit is taken so that all $(z_k-z_{k-1})\to 0$, the limit is unique for a given path.

   

2. For real functions of $x$ only, this corresponds to the usual (Riemann) integral, i.e. the area under the curve $f(x)$.
3. We have $$\int_C f(z)\,\d z=\int u\,\d x-\int v\,\d y+\ii\int v\,\d x+\ii\int u\,\d y=\int(u,-v)\cdot\d\mathbf{r}+\ii\int(v,u)\cdot\d\mathbf{r},$$ where $\d\mathbf{r}\equiv(\d x,\d y)$. The last two integrals are real line integrals in the $xy$-plane.
4. Reversing the direction of the contour changes the sign of the integral.
5. For compound curves, $$\int_{C_1+C_2} f(z)\,\d z=\int_{C_1} f(z)\,\d z+\int_{C_2} f(z)\,\d z\qquad\text{and}\qquad\int_{C_1-C_2} f(z)\,\d z=\int_{C_1} f(z)\,\d z-\int_{C_2} f(z)\,\d z.$$
6. The estimation lemma states $|\int_C f(z)\,\d z|\le ML$ where $L$ is the length of the curve and $M$ is the maximum value of $|f(z)|$ along the curve.
7. A Jordan curve is a closed, non-self-intersecting curve. The integral along such a curve is denoted by $\oint$, and is taken in an anticlockwise direction by default.

Riley 18.10; (Boas 14.3); Arfken 6.3